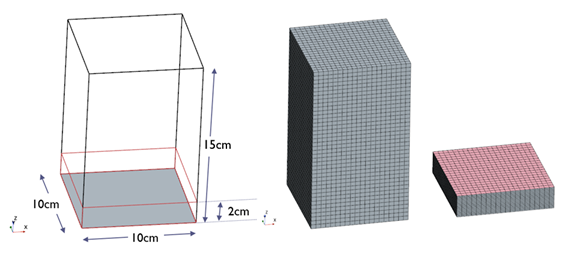
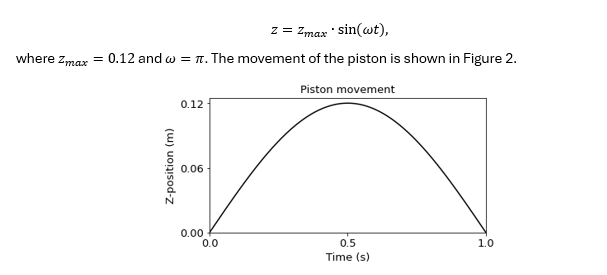
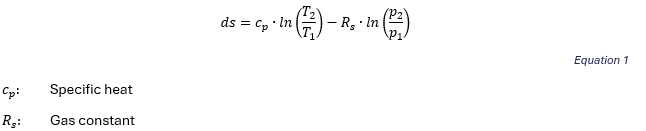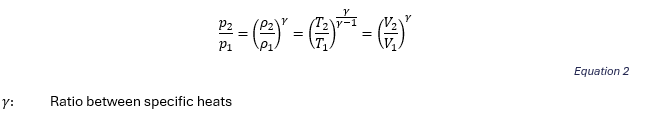Results
The video below is provided to get an insight into the workings of the overset mesh.
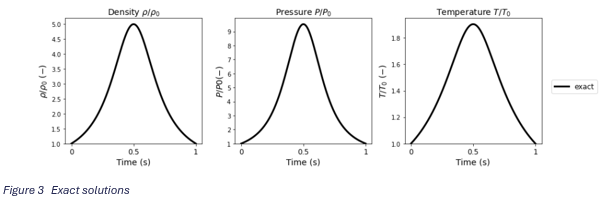
A comparison is made between the exact solution and the simulation results. The graphs below show the average density, pressure and temperature over the domain for the different overset mesh conservation setting. The exact solution is also plotted in the graphs.
The results shown in Figure 4 are from simulations with a relatively large timestep (dt = 0.01). Even though the mass tracking option yields better results in computing the compression rates, a slight lagging phase shift is present. When the timestep is halved (dt = 0.005), this phase shift decreases. This can be seen in Figure 5. The results for the other mesh conservation settings also improve, but not sufficiently.
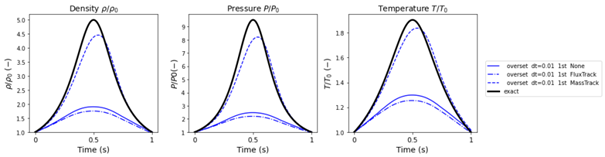
Figure 4 Results (with timestep: dt = 0.01)
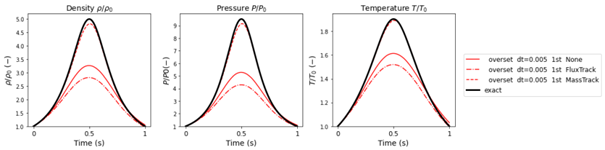
Figure 5 Results (with timestep: dt = 0.005)
The graphs clearly indicate that the results only come close to the exact solution when the mass tracking option is used. However, none of the overset conservation options provide a perfect solution. Interestingly, the flux tracking option does an even poorer job of conserving the mass during the simulation than having no overset conservation option at all.
The reason for the poor performance of the flux correction has to do with the acceptor-to-active cells boundary. In an overset mesh the acceptor cell is a sort of “ghost cell” which receives information from all overlapping background mesh cells through the chosen interpolation scheme. The active cell then gets this information from the acceptor cell which is then used within the simulation. The flux correction enforces the mass flux through the acceptor-to-active cells boundary to be zero and implements this in the pressure-correction equation. This boundary is defined by the overset interface in the region and the number of zero-gap layers. In this case, this boundary is located 2cm above the valve surface, as shown in Figure 6.
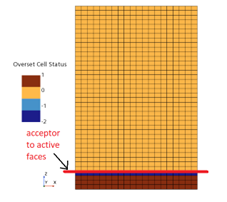
Figure 6 Acceptor-to-active cells boundary
Technically, a mass sink is located at this boundary in the domain 2cm away from the valve surface. In reality, mass should be able to move through these faces. A remedy could be to bring the overset interface closer to the valve surface. However, this also means that the background mesh needs to be refined to keep sufficient number of cells for the ZeroGap cell layer requirement. The density does return to at the end of the simulation, which means that no mass is lost.
In contrary to the flux correction, mass tracking acts as a mass source rather than a sink. This source is added to the continuity equation. This is different than for the flux correction implementation where the pressure correction equation is modified. The mass tracking overset conservation corrects the mass at a certain point in time relative to the amount of mass that was initially present in the system. The difference in mass is added as a source term to the continuity equation.